LIFE HISTORY EVOLUTION
For each organism a story can be told about how it makes a living. Most
of the traits that are part of this story have genetic bases and they contribute
to fitness in some way. Usually in the context of life history
strategies fitness is discussed in the context of different growth
rates. New mutations that alter the growth rate-related traits of organisms
should lead to the evolution of new life histories.
A few stories: the agave plant lives for many/several years in
the harsh desert environment and when sufficient rain occurs it sends up
a tall reproductive structure, flowers, seets seed and dies. The codfish
after reaching sexual maturity may produce a million eggs in a reproduction,
and do so over several seasons; species of salmon forego reproduction
until a late age, swim up current in certain rivers/streams, sink all of
their digestive tract and much of their muscle mass into eggs in one reproductive
effort, and die. Marine invertebrates: viviparous species have 20-100
offspring, primitive brooders have 100-1000 eggs/offspring, species
with no parental care have 1000-500,000,000 eggs (Aplesia,
sea slug). How these different species achieve these feats is one
question (a physiological one). Why they do it is a very different
one and difficult to answer. We address this question by analyzing life
history strategies.|
Best done by considering components of life history 1) survivorship
and 2) reproduction. Two further questions: 1) what is the best
relative allocation of resources to each of these components, 2)
what is the best timing of reproduction?
G. C. Williams suggested that there is a trade-off between survival
and reproduction: if one puts more resources into survival then there are
fewer resources remaining for reproduction. Conversely, reproduction
is costly and will reduce survivorship in subsequent years and
reduce the future reproductive output.

The bigger they get the more eggs they can produce. This presents a
dilemma: when should they reproduce?; now so they don't miss out?, later
so they can produce more? but what if they get killed? if they are going
to die anyway why not now? how many eggs?, etc., etc. These are the questions
facing the existential poker player. One starts with a given number
of chips (~ egg yolk), how does one play one's cards? how does one invest
one's chips (~ resources during growth and development)? when does one
decide to "fold" (wait until next year to reproduce when the
conditions might be better, new hand ~ random set of new environments)?
what cards do the other players hold (~ unknown variables of the biotic
environment ~ competitive abilities of the other "players").
All of these questions assume that the strategies have some high fitness solution. Lets consider growth rate as one measure of a given genotype's (~ individual) fitness.
| time | 0 | 1 | 2... | t |
| population size (at time t) | N(0) | N(1) | N(2) | N(t) |
| growth parameter | l | l | l |
N(1) = N(0)l => l = N(1)/N(0); similarly N(t) = N(0)lt => lt = N(t)/N(0)
This can be converted to an instantaneous growth rate using an exponential: N(t) = N(0)ert where r is comparable to l . The point is that different genotypes could have different l 's and hence different fitnesses; selection = the difference between genotypes in their growth rates.

We can describe the net reproductive rate (Ro)
of a genotype or individual in terms of its age specific survivorship
and fecundity: x = age, lx = probability of surviving
from age 0 to age x, mx = number of offspring produces by an
individual of age x. Ro = lx
mx = expected total offspring per female during her lifetime.
Now we can Calculate an lx mx table, or life table.
| Age | lx | mx | #offspr | lx' | mx' | #offspr' |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0.5 | 1 | 0.5 | 0.5 | 0 | 0 |
| 2 | 0.4 | 4 | 1.6 | 0.4 | 1 | 0.4 |
| 3 | 0.2 | 4 | 0.8 | 0.2 | 4 | 0.8 |
| 4 | 0.1 | 2 | 0.2 | 0.1 | 4 | 0.4 |
| 5 | 0 | 0 | 0 | 0 | 2 | 0 |
| Ro = | 3.1 | Ro = | 1.6 |
Note that the right hand column (a hypothetical new genotype called
') has the same lx schedule and the same mx schedule
except that it has been moved down one year (start reproducing later).
The genotype with the earlier age of first reproduction has the
higher net reproductive rate. This genotype will outcompete the other (')
and selection acting on such strategies will have the effect of
reducing the age of first reproduction because those genotype with
thes trait (early reprod.) will have higher growth rate = fitness. This
approach (lx mx) helps us identify those components
of a life history that might affect fitness and hence be selected for/against.
Charnov and Schaefer proposed a simple model to examine whether annuals
(species living one year) or perennials (species living more than
one year) should be favored. P = number of progeny that survive
to reproduce (including the parent in the perennial case), B = number
of seeds produced, S1 = survival during first
year of growth, S2 = survival during subsequent
years (subscript a = annual, p = perennial). for the annual: Pa = BaS1;
for the perennial: Pp = BpS1+S2.
Now we wont to n=know when is Pa > Pp
(i.e., when is the reproductive output of the annual greater than that
of the perennial?) Answer = when BaS1
> BpS1+S2.
Rearrange to find that the annual habit will be favored when Ba
- Bp > S2/S1
In english this means that for the annual habit to be favored it has
to have a reproductive output greater than the perennial by the amount
S2/S1 (i.e., the ratio of the
"old" survivorship to the "young" survivorship. The
result fits well with observations about where annual and perennial plants
are found: many desert plants are annuals (low probability of survivorship),
perennials common in tropics).
Other issues that might affect the evolution of life history traits:
Certain environments (arctic) dramatic changes in weather/seasons can cause
lots of death in a genotype independent manner (in an extreme case).
Selection that goes on might be more effective in the growth phase
after population crash; this would select for genotypes that have high
rates of reproduction (r), so-called r-selected species/genotype/traits
(rapid development, early reproduction, small body size, semelparity
[reproduce once]). In more stable environments, where the population
might be near its maximum size, selection favors competitive ability
to survive at the "carrying capacity" (= K) of the population;
such species/genotype/traits are said to be K-selected (slow development,
reduced resource requirement, delayed reproduction, large body size, iteroparity
[reproduce more than once]). This is best thought of a a continuum
since species are not either/or.
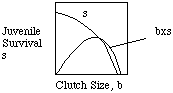
Another important way of thinking about life histories is bet hedging where variable environments don't allow for the evolution of one particular strategy. Consider the evolution of optimal clutch size ( how many eggs should I lay?). Again, the trade off between survivorship and reproduction may determine one clutch size, but in a variable environment, clutch sizes tend to be lower because there is an increased risk of losing an average investment in reproduction. A slightly smaller clutch can lead to a higher net reproductive rate (Ro)because it can allow for more reproductive seasons than might be physiologically possible with larger clutch sizes. This argument applies iteroparous organisms; the bet hedging in a semelparous orgnanism might involve hedging on how long to wait before reproducing because semelparous breeders will not have another clutch.
Other alternative strategies for dealing with spatial and temporal heterogeneity
Dormancy (wait out the bad times; seeds are good life history
strategy here; an associated strategy is responding to appropriate environmental
cues for growth). Dispersal (spreading the risk in unpredictable
environments; fruits (carrying seeds) again good examples;
aphids, crickets respond to crowding by producing wings and dispersing.
The life table approach shows us that individuals of different ages are not "worth" the same in terms of reproductive potential. A newborn at time 0 when population size = N(0) is 1/N(0) of the population. In the next time interval the population has grown so a newborn is 1/N(0)l of the population and relative to a newborn at time 0, this newborn is "worth" = (1/N(0)l)/(1/N(0)) = 1/l = l-1. Similarly a newborn born at time t is 1/N(0)lt of the population and relative to a newborn at time 0 it is "worth" = (1/N(0)lt)/(1/N(0)) = 1/lt = l-t. Since the population is growing, a newborn born at a later age is a smaller proportion of the population. This means that older individuals contribute less to the makeup of the population. Also, older individuals may be a smaller proportion of the pool of reproductive adults, so they contribute even less to the population. The net effect is that the reproductive value of older individuals is less than that of younger individuals. Reproductive value of an individual is the contribution to future generations of an individual of age a. It can be quantified as
Va = (la / la) lxlxmx
Another way to think of this is the age distribution of test tubes
in a lab: more new one than old ones, associated with ageing is a finite
probability of being broken, thus a smaller proportion of all test tubes
in the lab will be veery old. These old one will not contribute much to
"next generation"
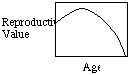
Two points: 1) reproductive value may increase from birth to
first reproduction (in species that delay reproduction) because as one
survives to this age, one increases the probability that one will actually
reproduce; 2) the drop in reproductive value with age can account for the
evolution of senescence (physiological decay with age).
Obviously genes for physiological decay would be selected against. But
if ageing is due to the expression of "decay" genes late in life,
selection will not be able to act on them because the genotypes which express
this phenotype (decay) have very little reproductive value at that age.
Extreme example: a gene for death at age 80 could not be selected out of
the population unless individuals were reproductively active past
this age. If you stop reproducing before age 80 selection will not result
in differential survival of genotypes via phenotypic selection.